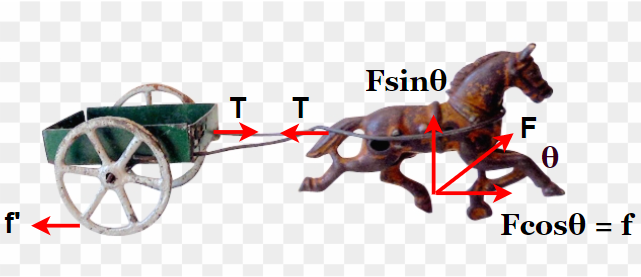
When a horse pulls the cart, then, according to Newton’s Third Law, the cart also pulls the horse backwards with an equal force. It seems like the horse should not move, but we know that there is always a motion. So, what’s going on?
In the process, the horse pulls the cart with force T ( this force is called ‘Tension’ since the force is transmitted through the rope), and the cart pulls the horse with an equal force T in the opposite direction.
Acceleration of the horse
In order to move, the horse presses the ground in the inclined way, and the ground provides the equal reaction force ‘F’ as shown in the figure.
This force ‘F’ is known as ‘contact force’. Let it be inclined at angle θ with the horizontal.
The vertical component ‘Fsinθ’ balances the weight ‘mg’ of the horse, and the horizontal component ‘Fcosθ’, also known as ‘frictional force’ provides the necessary acceleration overcoming the tension, T, on the rope connecting the horse and the cart (Yes, it is friction that helps everyone of us move forward!).
Let us denote Fcosθ by f.
If f > T, then the horse gains an acceleration ‘a’ in the forward direction. Then,
Fcosθ -T = ma
f – T = ma
a = (f – T)/m ….. (1)
Acceleration of the cart
In case of cart, the tension T pulls the cart in the forward direction, and a friction f’ acts in the backward direction. Let the cart of mass m’ move with acceleration a’. Then,
T – f’ = m’a’
a’ = (T – f’)/m’ …..(2)
Combined Motion
Forces f and f’ in equation 1 and equation 2 respectively are self adjustable forces. During the motion, they adjust in such a way that the acceleration of both, the horse and the cart, is equal, i.e.
a = a’
(f – T)/m = (T – f’)/m’
In this way, the horse and the cart move in the forward direction.
Was this blog helpful? Mention in the comments section below.
Do not forget to check our other blogs, and research paper summaries.