Here’s a bet!

I will flip a coin. If it is head, I will give you Rs. 1000, but if it is a tail you will have to give me Rs. 500.

Would you take it?

Chances are, you would hesitate. But, let me tell you something, any rational human being would take it. This discrepancy between what’s rational and how we behave is what we will account in this article introducing a ground breaking theory called Prospect Theory.

Introduction

In the paper, “Prospect Theory: An Analysis of Decision Under Risk” published on Econometrica on March 1979, Nobel Prize winning economist Daniel Kahneman, and Amos Tversky presented ‘a critique of Expected Utility Theory’ saying that it cannot be taken as an adequate descriptive model for decision making under risk, and developed an alternative model called Prospect Theory.

Expected Utility Theory

This is a theory of utility in which ‘betting preferences’ of people with regard to uncertain outcomes (gambles) are represented by a function of payouts and the probabilities of occurrence. This means, when confronted with a decision involving risk, people behave rationally and pick a decision with a higher expected utility.  

However, Kahneman and Tversky found that the choices of the people violate the principle of expected utility theory. People tend to overweight the outcomes that are considered certain as compared to the outcomes which are merely probable (certainty effect). Because of this, people become risk-averse in choices involving sure gains and risk-seeking in choices involving sure losses.

To clarify the concept, let’s consider the following gambles:

92 % of the respondents preferred Gamble C. If we calculate the expected utility,

Expected utility for Gamble C = – 3200

Expected utility for Gamble D = – 3000

Clearly, people should select Gamble D since it has a greater expected utility. But again, that was not the case! People choosing gamble C over D clearly shows that people become risk-seeking in case of sure losses.

The first set of cases above (A & B) deals with gains, and the second set (C & D) with losses, i.e. the signs of the outcomes have been reversed. Doing so, we can see that the preferences of the respondents have also been reversed. This phenomenon is called The Reflection Effect.

Prospect Theory

Prospect Theory explains why people behaved differently than what was predicted by Expected Utility Theory. Prospect Theory assumes that :

1. People assign value to gains and losses (from some reference point) rather than to final assets.
2. Their decision is not based upon the actual probabilities, but on the decision weights (which are effectively the psychology induced probabilities).

i. The Value Function

As stated above, the essential feature of the prospect theory is that the carriers of value are changes in wealth or welfare, rather than their final states. This is a strong argument because the same level of wealth, for example, may imply abject poverty for one individual and great riches for another – depending upon their current assets (reference point).

Kahneman and Tversky hypothesized that the value function is normally concave for gains and convex for losses, and is generally steeper for losses than for gains, as shown in the figure below:

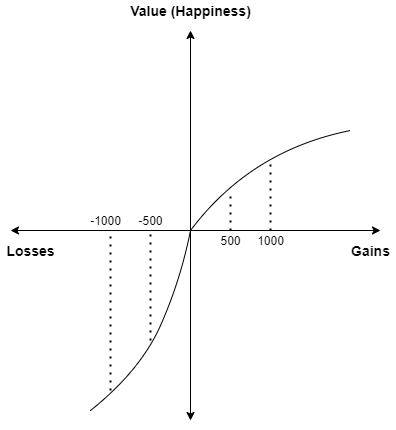
To understand better the value function, let’s come back to a betting question that we asked at the beginning of the article.

There is a 50% chance that you will win 1000, and there is a 50% chance that you will loose 500. Therefore,

0.5 * 1000 – 0.5 * 500 = some positive value

Clearly, this betting option has a positive expected value and you should take it without any second thought. However, your erroneous heuristic plays the role of spoilsport.

If we assign happiness to be the value, then from the above curve we can see that the level of happiness we experience if we gain 1000 is lower than the corresponding level of sadness that we experience if we loose 500. (Again, I would like to emphasize that gain of 1000 and loss of 500 are not important in themselves. What’s important is the percentage change from the reference point – your current assets. Those numbers could be 100 and 50 for a little child, and 10,00,000 and 5,00,000 for a rich businessman.)

ii. Decision Weight

Decision weight is another important aspect of prospect theory. It is a function which illustrates that people have the psychological tendency to tweak the actual probability.

If the occurrence of an event has a very low probability then our brain is likely to ignore the little probability, and calls it an event with zero probability. Likewise, if the occurrence of an event has a very high probability, then our brain rounds it to 1.

However, in the cases when our brain does not automatically round the small probabilities to 0 and larger probabilities to 1, it is likely to overweight and underweight the values respectively as seen at the point of discontinuity on the left and right side of the figure 2. For example, even though the air travel is the safest means of transportation, people are always likely to overestimate the probability of a crash.

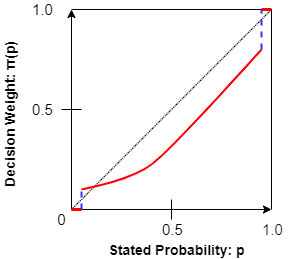
As people are limited in their ability to understand and evaluate extreme probabilities, highly unlikely events are either ignored or overweighted, and the difference between high probability and certainty is either neglected or exaggerated.

The curve of the decision weight (psychology-induced probability) vs actual probability is non-linear. The dotted line in figure 2 is only when we are completely rational and put emotions aside while decision making. The following example explains the non-linearity of the curve.

Consider that you are given an opportunity to purchase the removal of one bullet from the loaded gun. Would you pay as much to reduce the number of bullets from four to three as you would to reduce the number of bullets from from one to zero? Even though the change in probability of death is same, most people feel that they would be willing to pay much more for a reduction of the probability of death from 1/6 to zero than for a reduction from 4/6 to 3/6 (Assuming, the gun can accommodate six bullets).

Conclusion

Unlike Expected Utility Theory, Prospect Theory takes into account how our emotions affect our decision making. A rational decision is the one where we will decide solely on the basis of expected utility. However, our own emotions drag us into the irrational school of thought inviting us to make erroneous decisions. All the leadership and corporate trainings in the current world are targeted to reduce this error.

Was this summary helpful?

Mention in the comments section below.

Do not forget to check our other research paper summaries, and general blog posts.